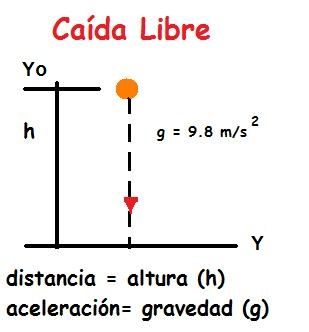
caída libre
El movimiento de los cuerpos en caída libre (por la acción de su propio peso) es una forma de rectilíneo uniformemente acelerado.
La distancia recorrida (d) se mide sobre la vertical y corresponde, por tanto, a una altura que se representa por la letra h.
En el vacío el movimiento de caída es de aceleración constante, siendo dicha aceleración la misma para todos los cuerpos, independientemente de cuales sean su forma y su peso.
La presencia de aire frena ese movimiento de caída y la aceleración pasa a depender entonces de la forma del cuerpo. No obstante, para cuerpos aproximadamente esféricos, la influencia del medio sobre el movimiento puede despreciarse y tratarse, en una primera aproximación, como si fuera decaída libre.
La aceleración en los movimientos de caída libre, conocida como aceleración de la gravedad, se representa por la letra g y toma un valor aproximado de 9,81 m/s2 (algunos usan solo el valor 9,8 o redondean en 10).
Si el movimiento considerado es de descenso o de caída, el valor de g resulta positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de ascenso en vertical el valor de gse considera negativo, pues se trata, en tal caso, de un movimiento acelerado.
Para resolver problemas con movimiento de caída libre utilizamos las siguientes fórmulas:

Fórmulas del Movimiento de Caida Libre
a). V = Vo +- gt (si es caida se suma el producto gt, si el cuerpo sube se resta el producto gt)
Ojo el signo menos de la gravedad depende si el cuerpo sube o baja. Si el cuerpos subiera la gravedad actuaría en contra de su movimiento. si el cuerpo cae la gravedad actuaría a favor del movimiento
b). Vm = (vo + v)/2C
c). Y = -0.5 gt² + vo t + Yo
d). v²= -2gt (Y - Yo)
Donde V es velocidad final, g la gravedad (en la tierra 9,8m/s), Vo velocidad inicial, Vm velocidad media, t es el tiempo, la y es la altura final (si cae en el suelo será cero), la Yo es la altura inicial desde donde se suelta el objeto. Ojo en algunos libros veremos como a las Y se les llama h o altura.
Ejemplo N º 2
Supongamos que un objeto se lanza verticalmente hacia arriba, desde la parte superior de una torre:
CASO I
Ubicamos el sistema referencial en el piso.
“Yo”: es igual a la altura de la torre
“Y” : es la altura máxima que alcanza el objeto, medido desde el punto de partida, (pero en el resultado hay que tener en cuanta la altura de la torre mas lo que sube el objeto producto de la fuerza que se le impuso al lanzarlo)
Para ese instante la velocidad del objeto vale cero.
“Y” será igual a la altura de la torre, pero con signo negativo; cuando se pregunta por el tiempo que tarda en tocar el piso o la velocidad al llegar al piso.
CASO II
Ubicamos el sistema referencial en la parte superior de la Torre.
“Yo”: es igual a cero
“Y” : es la altura máxima que alcanza el objeto, medido desde el punto de partida, (pero para el resultado hay que tener en cuenta la altura de la torre mas lo que sube el objeto producto de la fuerza que se le impuso al lanzarlo)
Para ese instante la velocidad del objeto vale cero.
“Y” será igual a la altura de la torre, pero con signo negativo, cuando se pregunta por el tiempo que tarda en tocar el piso o la velocidad al llegar a este.
Resolver los siguientes problemas:
Problema n° 2) Si se deja caer una piedra desde la terraza de un edificio y se observa que tarda 6 s en llegar al suelo. Calcular:
a) A qué altura estaría esa terraza.
b) Con qué velocidad llegaría la piedra al piso.
Respuestas:
a) 180 m
b) 60 m/s
Supongamos que un objeto se lanza verticalmente hacia arriba, desde la parte superior de una torre:
CASO I
Ubicamos el sistema referencial en el piso.
“Yo”: es igual a la altura de la torre
“Y” : es la altura máxima que alcanza el objeto, medido desde el punto de partida, (pero en el resultado hay que tener en cuanta la altura de la torre mas lo que sube el objeto producto de la fuerza que se le impuso al lanzarlo)
Para ese instante la velocidad del objeto vale cero.
“Y” será igual a la altura de la torre, pero con signo negativo; cuando se pregunta por el tiempo que tarda en tocar el piso o la velocidad al llegar al piso.
CASO II
Ubicamos el sistema referencial en la parte superior de la Torre.
“Yo”: es igual a cero
“Y” : es la altura máxima que alcanza el objeto, medido desde el punto de partida, (pero para el resultado hay que tener en cuenta la altura de la torre mas lo que sube el objeto producto de la fuerza que se le impuso al lanzarlo)
Para ese instante la velocidad del objeto vale cero.
“Y” será igual a la altura de la torre, pero con signo negativo, cuando se pregunta por el tiempo que tarda en tocar el piso o la velocidad al llegar a este.
Resolver los siguientes problemas:
Problema n° 2) Si se deja caer una piedra desde la terraza de un edificio y se observa que tarda 6 s en llegar al suelo. Calcular:
a) A qué altura estaría esa terraza.
b) Con qué velocidad llegaría la piedra al piso.
Respuestas:
a) 180 m
b) 60 m/s
Tiro Parabólico
El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (M.R.U.A) por la acción de la gravedad.
Física
Cinemática: Tiro parabólico. Ecuaciones de la trayectoria. Velocidad, espacio y aceleración. Movimiento rectilíneo uniforme. Movimiento uniformemente variado.
Tiro parabólico
Se trata de un “movimiento rectilíneo uniforme” en su desarrollo horizontal y un “movimiento uniformemente variado” en su desarrollo vertical. En el eje vertical se comporta como el movimiento de “Tiro vertical”.
Otro tipo de movimiento sencillo que se observa frecuentemente es el de una pelota que se lanza al aire formando un ángulo con la horizontal. Debido a la gravedad, la pelota experimenta una aceleración constante dirigida hacia abajo que primero reduce la velocidad vertical hacia arriba que tenía al principio y después aumenta su velocidad hacia abajo mientras cae hacia el suelo. Entretanto, la componente horizontal de la velocidad inicial permanece constante (si se prescinde de la resistencia del aire), lo que hace que la pelota se desplace a velocidad constante en dirección horizontal hasta que alcanza el suelo. Las componentes vertical y horizontal del movimiento son independientes, y se pueden analizar por separado. La trayectoria de la pelota resulta ser una parábola.
Es un movimiento cuya velocidad inicial tiene componentes en los ejes "x" e "y", en el eje "y" se comporta como tiro vertical, mientras que en el eje "x" como M.R.U.

El tiro parabólico tiene las siguientes características:
- Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales.
- La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
- Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
- Se puede analizar el movimiento en vertical independientemente del horizontal.
Se patea un balón de fútbol con un ángulo de 37° con una velocidad de 20 m/s. Calcule:
a) La altura máxima.
b) El tiempo que permanece en el aire.
c) La distancia a la que llega al suelo.
d) La velocidad en X y Y del proyectil después de 1 seg de haber sido disparado
Dato
Ángulo = 37°
|
a) Ymax = ?
|
d) Vx =?
|
Vo = 20m/s
|
b) t total = ?
|
Vy = ?
|
g= -9.8 m/s^2
|
c) X = ?
|
1:- Vox = Vo Cos a = 20 m/s Cos 37° = 15.97 m/s
Voy = Vo Se n a = 20 m/s Sen 37° = 12.03 m/s
Paso 2
Calcular el tiempo de altura máxima , donde Voy = 0
Por lo tanto : t = (Vfy - Voy) / g = (0 - 12.03 m/s) / 9.8 = 1.22.seg.
Paso 3
Calcular a) la altura máxima:
Ymax = Voy t + gt^2 / 2= 12.03 m/s ( 1.22s) + (( -9.8m/s^2 )(1.22s)^2) / 2 = 7.38m
Paso 4
Calcular b) el tiempo total . En este caso solo se multiplica el tiempo de altura máxima por 2, porque sabemos que la trayectoria en este caso es simétrica y tarda el doble de tiempo en caer el proyectil de lo que tarda en alcanzar la altura máxima.
T total = tmax (2) = 1.22s (2) = 2.44 s.
Paso 5
Calcular el alcance máximo, para lo cual usaremos esta formula:
X = Vx t total = 15.97 m/s ( 2.44s) = 38.96 m.
Paso 6
Vfy = gt + Voy = (- 9.8) ( 1seg.) + 12.03 m/s = 2.23 m/s
Vfx = 15.97 m/s ,ya que esta es constante durante todo el movimiento
Voy = Vo Se n a = 20 m/s Sen 37° = 12.03 m/s
Paso 2
Calcular el tiempo de altura máxima , donde Voy = 0
Por lo tanto : t = (Vfy - Voy) / g = (0 - 12.03 m/s) / 9.8 = 1.22.seg.
Paso 3
Calcular a) la altura máxima:
Ymax = Voy t + gt^2 / 2= 12.03 m/s ( 1.22s) + (( -9.8m/s^2 )(1.22s)^2) / 2 = 7.38m
Paso 4
Calcular b) el tiempo total . En este caso solo se multiplica el tiempo de altura máxima por 2, porque sabemos que la trayectoria en este caso es simétrica y tarda el doble de tiempo en caer el proyectil de lo que tarda en alcanzar la altura máxima.
T total = tmax (2) = 1.22s (2) = 2.44 s.
Paso 5
Calcular el alcance máximo, para lo cual usaremos esta formula:
X = Vx t total = 15.97 m/s ( 2.44s) = 38.96 m.
Paso 6
Vfy = gt + Voy = (- 9.8) ( 1seg.) + 12.03 m/s = 2.23 m/s
Vfx = 15.97 m/s ,ya que esta es constante durante todo el movimiento
Tiro horizontal
El lanzamiento horizontal es un tipo de movimiento que explica la interacción que tiene un "móvil" al estar en movimiento con una serie de factores físicos. Este movil durante su trayectoria tiene una serie de características específicas que lo diferencia de otro tipo de movimiento. Dichas características son:
- Tiene una relación directa con la "caída libre", la cual según Brett C., E., Suárez, W. A. (2012) "es el movimiento, en dirección vertical, con aceleración constante realizado por un cuerpo cuando se deje caer en el vacío".
- Este tipo de lanzamiento combina dos tipos de movimientos: el vertical (producido por la caída libre) y el vertical (definido como un Movimiento Rectilíneo Uniforme).* Ya que tiene dos movimientos, uno que atrae (la gravedad), y otro que hace mover al móvil hacia un lado “horizontal” (MRU), tenemos que la trayectoria es una semiparábola.

- Sí presenta un movimiento de caída libre, tenemos que la aceleración es la gravedad, la cual es: 9.8 m/s2.
- La Velocidad Inicial tiene solo componente horizontal, ya que la misma es accionada en sentido “horizontal” (valga la redundancia).
- La Velocidad dependerá de la altura del lanzamiento.
- La velocidad es aquella “distancia” que recorre el móvil en cierta cantidad de tiempo. Básicamente se calcula dividiendo la distancia recorrida entre el tiempo en que duro su trayecto. En este caso, tenemos dos tipos de velocidades en este lanzamiento, la velocidad “
Teoría :
El lanzamiento horizontal de un cuerpo corresponde a un movimiento unidimensional, en el cual la única fuerza que actúa sobre el cuerpo es la fuerza peso.
Consideremos un avión que vuela a cierta altura y quiere lanzar un paquete de víveres a unos náufragos en una isla.
El paquete de víveres experimenta un movimiento de bajada a lo largo del eje Y y un movimiento de avance a lo largo del ejeX.
- A lo largo del eje X es un MRU horizontal de velocidad Vox constante.
- En este tipo de lanzamiento la velocidad inicial, Vo, no tiene componente vertical, por lo tanto a lo largo del eje Y es un M.R.U.A debido a la gravedad terrestre.
- El origen del sistema de referencia lo tomaremos en el suelo debajo del lugar de lanzamiento.
Estas escenas han sido diseñadas de modo que el avión, una vez que lanza el paquete, inicia una maniobra evasiva ascendente.


Buen trabajo. Espero que sigas así gracias.
ResponderEliminar